|
THE CLIMATE OF EARLY MARS
|
I recently addressed the supposed scientific consensus regarding the origins and subsequent evolution of our Moon, including the significance of its impact history for our understanding of the Solar System as a whole. Scientific consensus turns out to be far more fragile than the popular media realise when they blithely report that “scientists have proven that …etc, etc “. However, astronomically speaking, the Moon is not alone in this regard: let’s take a look at Mars
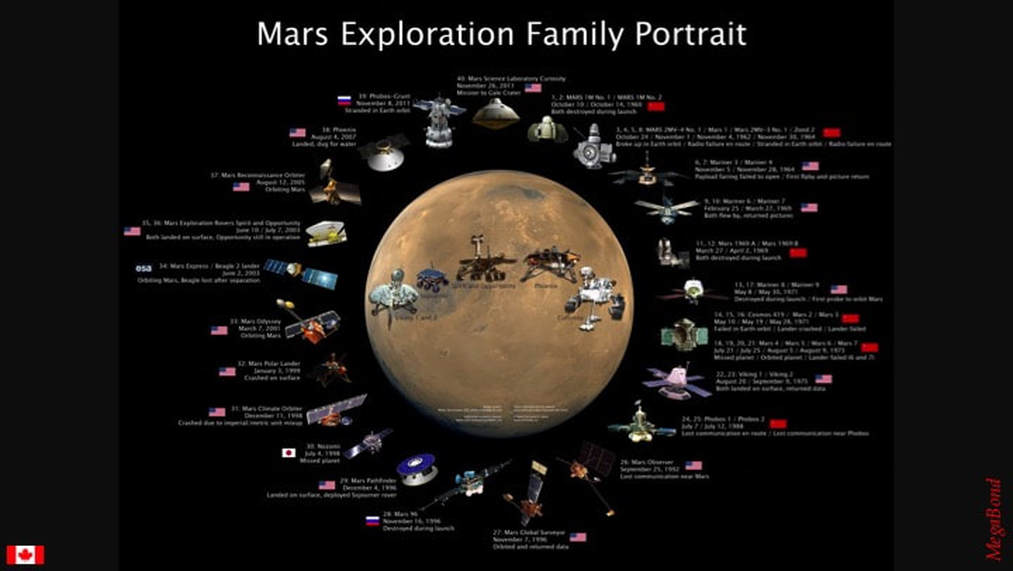
Given all the time and money that’s been poured into going to Mars since the early 1970s, you might think that some sort of scientific consensus regarding its history would have started to appear by now.
It’s true that we now have a really good idea of what its surface looks like …
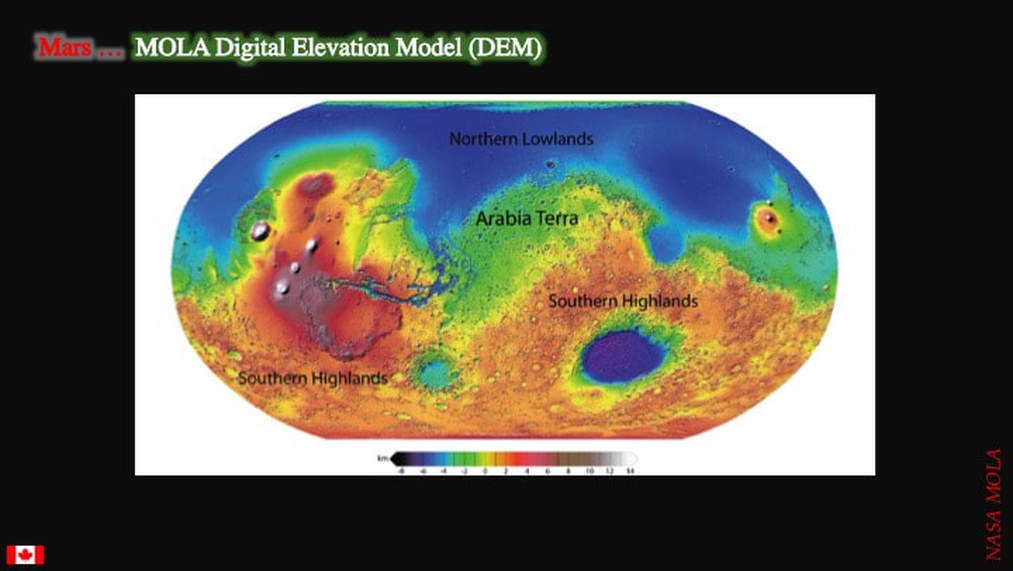
… and we can make very detailed digital elevation models (maps) of its topography that everyone can agree upon (red is high ground and blue is low ground).
We even have a pretty good idea of what the martian surface looks like at ground level.
But there are 2 fundamental questions currently driving our scientific activity regarding the red planet: was there ever standing water on its surface and did it last long enough for life to develop there? These four artists’ impressions of what a warm, wet Mars might have looked like prior to about 3.g billion years ago (~3.5 Ga: Noachian) are symptomatic of what a part of the planetary scientific community perceives regarding standing water. Note how the northern ocean represented here is blue. That implies liquid water around the North Pole - and that implies a warm climate, with a hydrological cycle of rainfall, rivers and streams, and lakes and deltas, all accompanied by clouds. A warm and wet early Mars is a perfectly valid hypothesis, supported by highly reputable scientists, and well worth taking seriously. However, over time it has come to be seen as the favoured model, bordering on consensus, at least until very recently.
For the past 18 months there has been a mounting open debate regarding the early climate of Mars, during the course of which many planetary scientists are promoting an alternative view. Instead of warm and wet, what if the early martian climate was in fact cold and dry ? This evolving scientific debate is on-going, and it remains unresolved. However, it is now maturing to the point where we as amateur astronomers can follow the reasoning on both sides of the discussion, and thereby participate, even if only as observers.
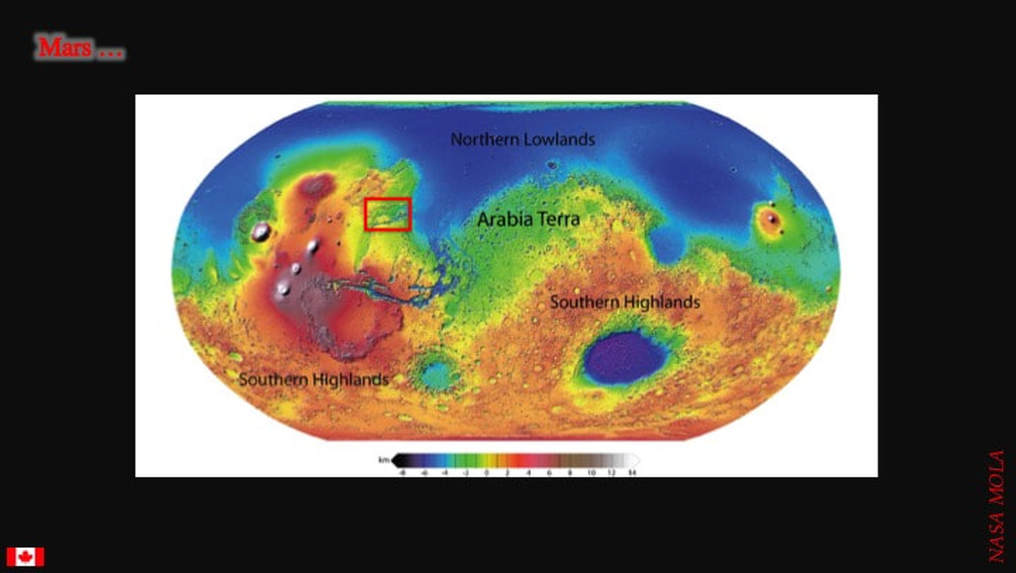
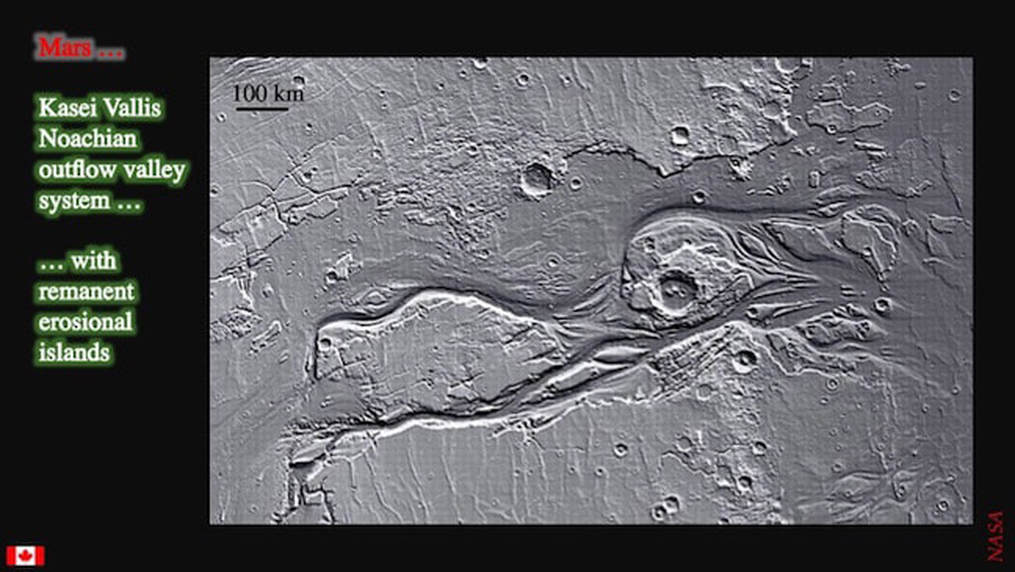
Let’s start by reminding ourselves what the warm and wet model, which has held sway for so long, is based upon: channels, lakes and a possible ocean. The channels come in all sizes, some of which can even be seen at the planet scale. The purported ocean pretty much coincides with the Northern Lowlands. The lakes are too subtle to see here, but we’ll look at them in just a moment. Meanwhile lets take a look at the NE end of Kasei Vallis, north of the Mariner Valley (red box).
Kasei Vallis is the largest outflow channel on Mars : it’s huge. This image serves to remind us of the kind of direct, observational evidence that exists for the erosive power of surface water on Mars. Note the multiple channels carved into the main channel, and the remanent erosional islands, both similar to features that can be seen all over the planet. However, Kasei Vallis is supposed to be the product of catastrophic, near-instantaneous erosion by flood waters. So while it clearly says “surface water”, it is not interpreted in terms of long-term surface water indicative of a warm and wet climate. So, what exactly does constitute evidence for long-term surface water? Lakes !
This is a false colour image of the Eridania Lake system, located in the Southern Highlands, just south of Gusev Crater where NASA’s Spirit Rover landed. Originally, it was the largest lake on Mars (1million km2) that then shrank to a system of smaller inter-connected lakes that linked to a lake in Gusev Crater via an outflow channel known as Ma’adim Vallis.
This lake system is relatively easy to identify from the flat lake beds that it left behind. However, other evidence for ancient lake beds on Mars is more equivocal.
Here’s an example. These three images are all interpreted as dried up lake bottom sediments that cracked into polygonal shapes. The one on the left is a textbook image from a known lake bed on Earth: note the scale bar. The next two images are from a dry lake bed in California and from a purported lake bed on Mars. The polygons are way bigger than the first example, but they are comparable in size: again, note the scale bars.
But a different scientific team interpreted the same martian example of polygons as the product of permafrost. Hardly a ringing endorsement of the lake bed interpretation. Maybe these two teams should talk to each other more !
So what about river systems ? Here’s a typical river system from Earth that shows tributaries converging and linking into larger channels that themselves link to the main river channel. The scale here is on the order of 100+ km, and establishing such an integrated fluvial system requires 1000s of years at least, thereby representing direct, observational evidence for medium- to possibly long-term surface water, even though it could be seasonal rather than uninterrupted flow.
This image from Mars – note the scale bar - has all the hallmarks of the terrestrial river system that we’ve just looked at. The inset is just a slightly wider field of view. Noachian examples of this from early Mars history occur in many places throughout the Southern Highlands.
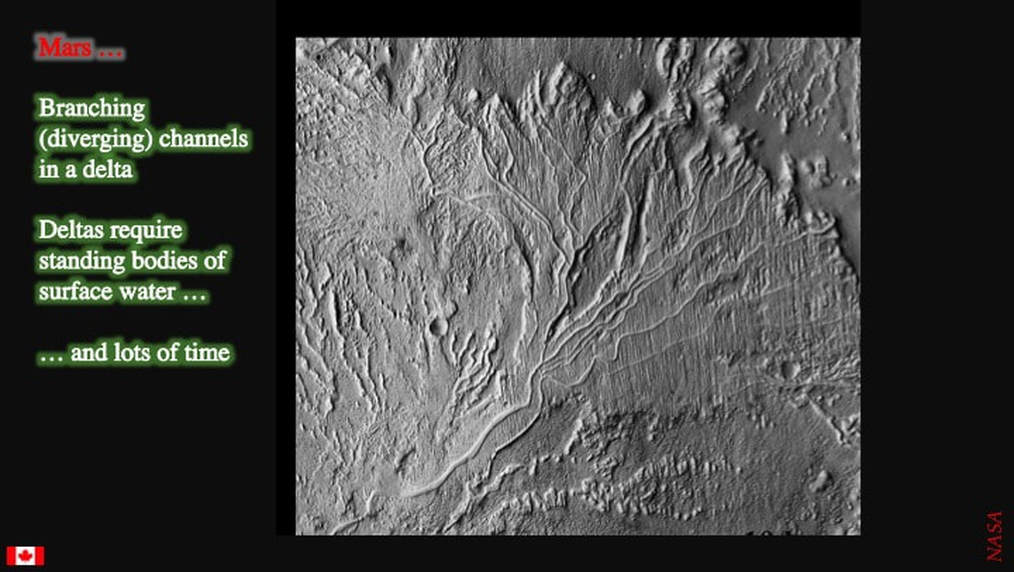
As I’ve explained in a previous presentation, where rivers empty into lakes, they slow down, dump the sediments they were transporting, and form deltas. The edge of this delta is visible at the top of the image, and you can readily see the river channel branching multiple times downstream toward the standing water of the lake. This is prima facie direct, observational evidence for medium- to long-term standing surface water. Again, Noachian examples of deltas from early Mars history occur in many places throughout the Southern Highlands.
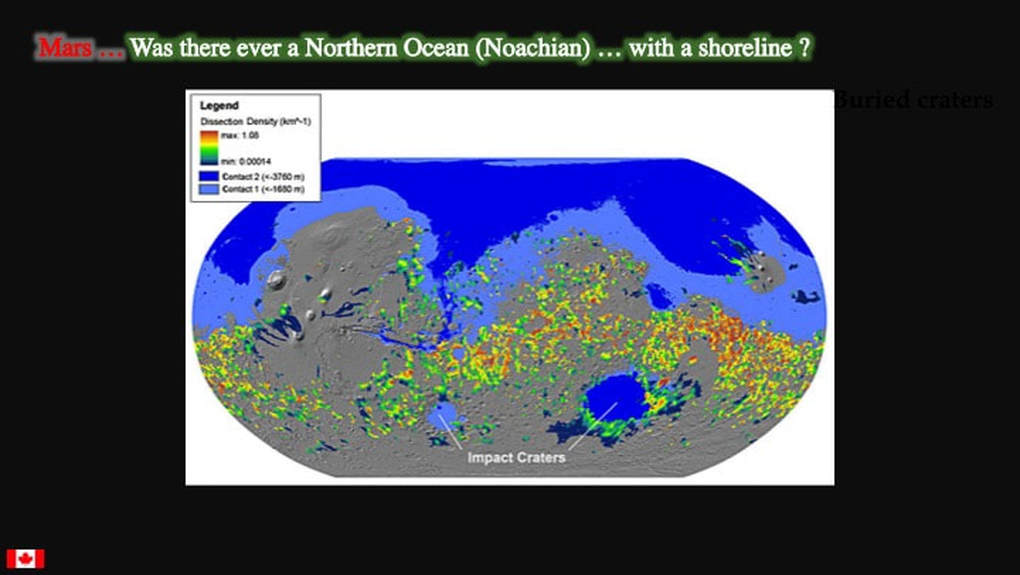
So much for channels, lakes, rivers and deltas, all of which require a certain amount of time to form and mature. However, the key witness to a truly long-term, globally wet planet would be the existence of an ocean whose time frame would be in the 100s of millions of years. Let’s be clear: the existence of this northern ocean is controversial to this day. Whatever, let’s briefly look at some of the observational evidence, for a shoreline at the boundary between the Southern Highlands (grey) and the Northern Lowlands (blue). The bright colours in this image reflect the distribution of ~40,000 north-flowing channels in the Southern Highlands, some of which have deltas at their northern ends, all marking the southern shoreline of the proposed ocean. Deviation of the supposed shoreline in the Tharsis uplift region can be readily explained in terms of later distortion by tectonic deformation.
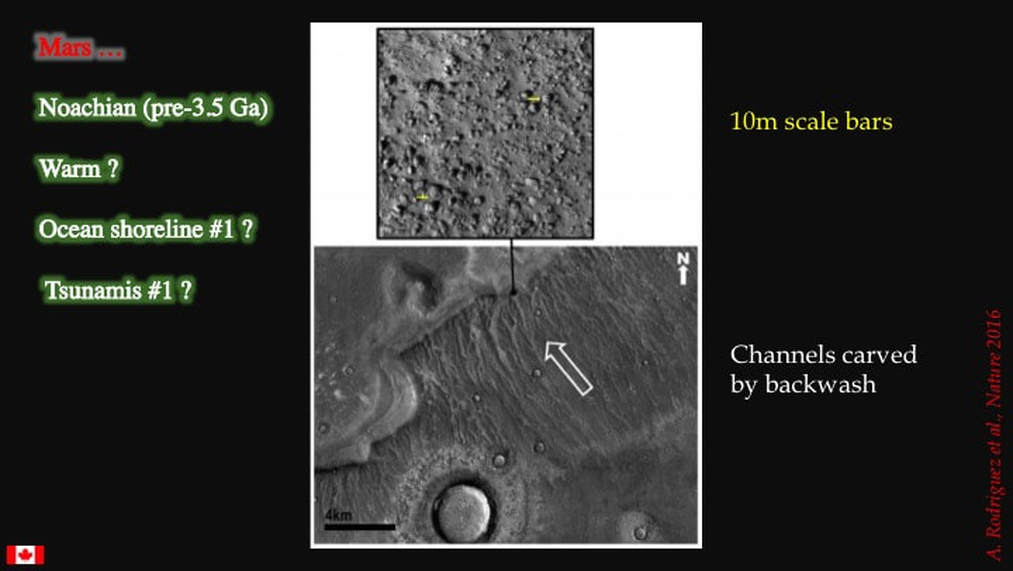
A very recent study ,published in 2016, interpreted the images shown here as fields of giant boulders (top : note scale) and large-scale channels along the southern edge of the proposed ocean, created by the incoming tidal wave and the out-going backwash of a tsunami resulting from a major meteor impact into the proposed ocean at ~3.5 Ga.
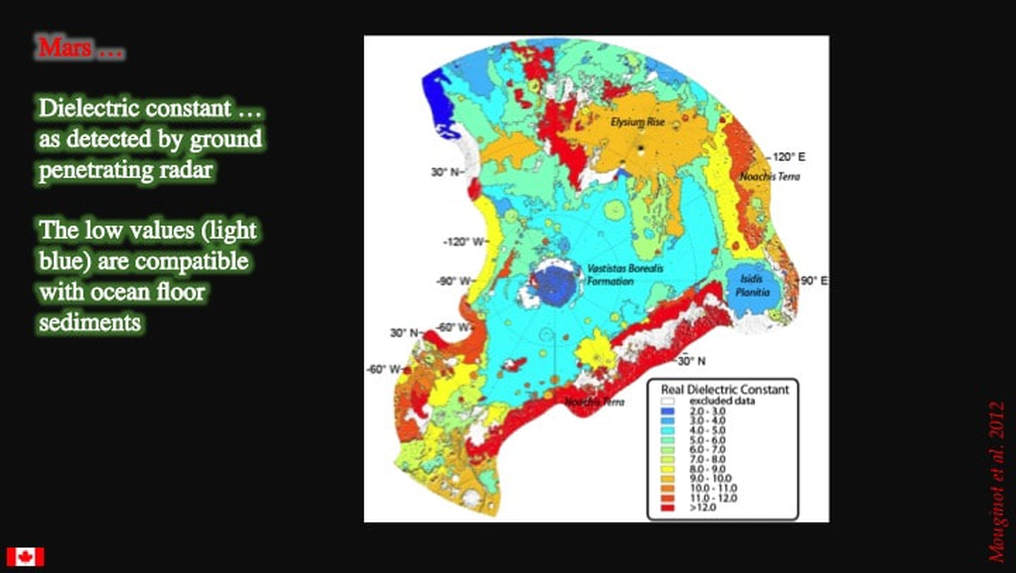
Finally, here’s some hi-tech evidence. This is a map of the martian North Pole region showing data from ground penetrating radar from ESA’s Mars Express orbiter. For those who like to know these things, dielectric constant refers to the ability of a material to concentrate or store an electrical flux or electrical energy. For the rest of us, it’s enough to know that the low values represented by the pale blue colour are best interpreted as indicating the presence of fine grained sediment; the kind of material you would expect to find accumulating on the floor of a large body of standing water – such as an ocean.
So, OK … we’ve got clear observational evidence for water on the surface of early Mars , including river systems, lakes and deltas, and pretty good observational evidence for the likely existence of an ancient ocean. So what’s the problem ? Why is the favoured warm and wet model, bordering on scientific consensus, being questioned today ?
Fundamentally the problem is this: Given the distance of Mars from the Sun, it receives ~45% less sunlight than we do on Earth. In addition, all models of solar (stellar) evolution propose that the early Sun was 25% fainter than it is today. Put these two elements together and Mars was inherently a cold place during the Noachian, i.e. prior to ~3.5 Ga. However, this is not in itself a problem. The issue is that computer-based climate models for early Mars – based on terrestrial climate models - fail to predict a greenhouse effect capable of generating a warm and wet climate. There are several variations on the general theme, using various mixtures of CO2, H2O, H2 and S, incorporating dust, aerosols and clouds at various atmospheric pressures, but all either fail or require very special conditions - otherwise known as special pleading. This has led some planetary scientists to suggest that perhaps the climate of early Mars was in fact cold and dry, but punctuated episodically by warmer conditions that lasted just long enough for the erosional and depositional landforms (e.g. rivers, lakes and deltas) to form. Some suggested that the heat derived from large meteor impacts onto a cold and dry Mars would generate a temporary steam atmosphere. Others have invoked outbursts of voluminous volcanism to temporarily “boost” the atmospheric greenhouse effect of a cold and dry Mars, and thereby a short-term hydrological cycle of rainfall, runoff, erosion and deposition.
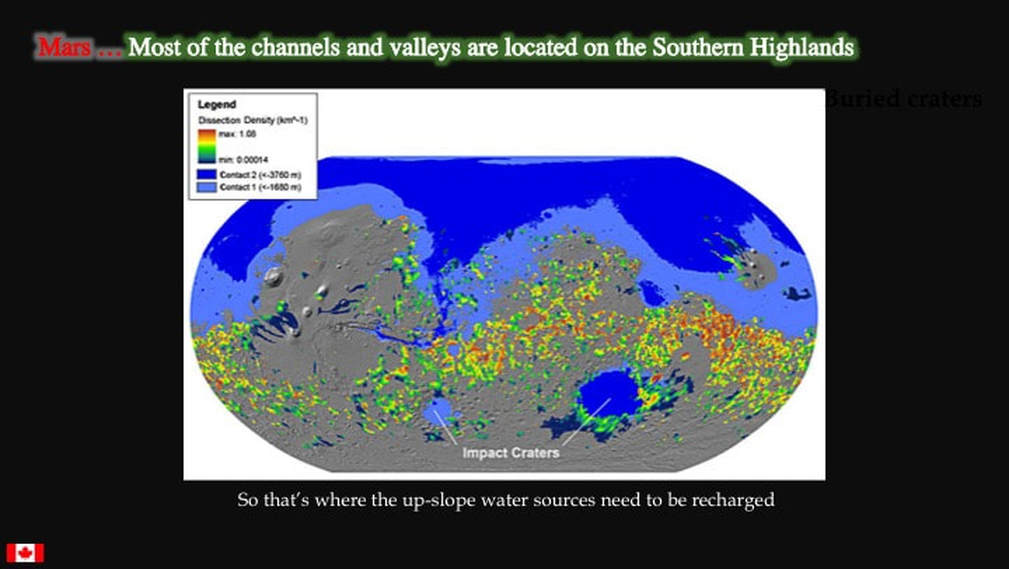
However, episodic wet conditions pose a major problem : water flows downhill! Once you’ve melted up-slope sources of water for one episode – however that is done - how do you recharge those source regions with more water in preparation for the next melting cycle ? This image clearly shows that since the channels and valleys are mostly found in the northern parts of the Southern Highlands, that’s where the source region recharge needs to occur. This is where we now enter the complex realm of climate modelling, but I’ll keep it as simple as possible. Please Note : we’re going to have to ignore the northern ocean for a while, but I will come back to it at the end !
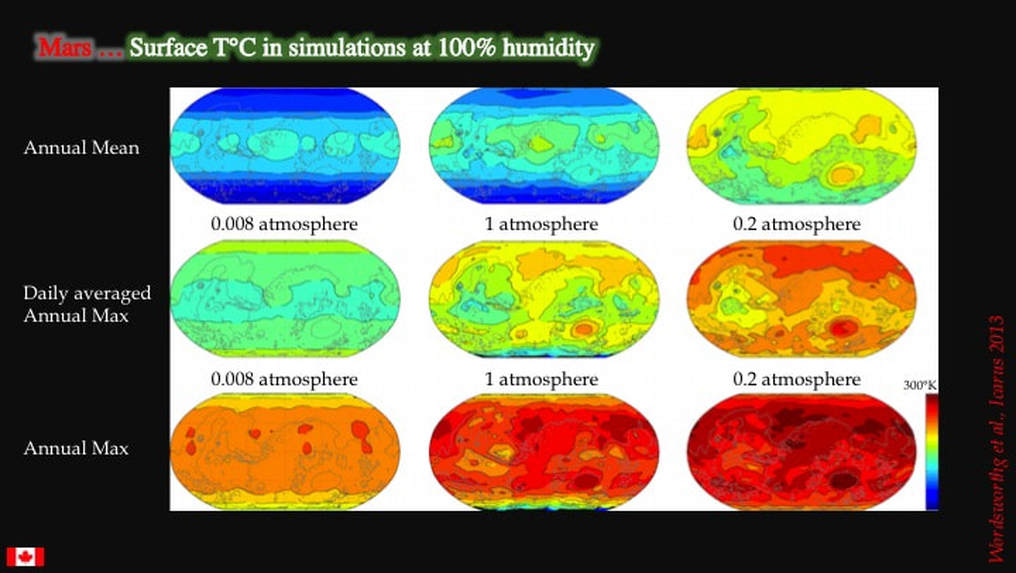
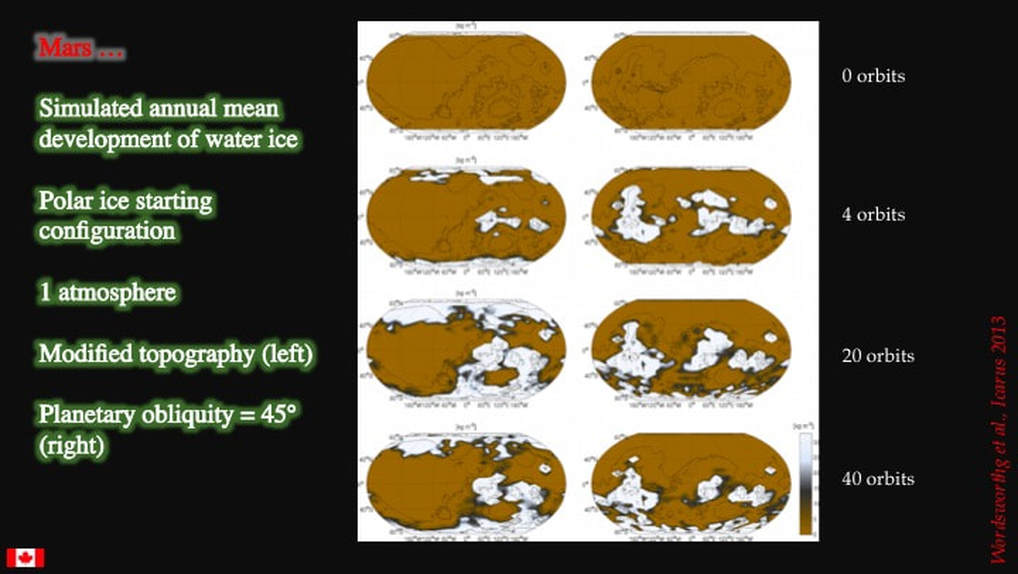
Since 2012, a group of planetary scientists has been publishing a series of papers where they specifically address the question of recharging up-slope water sources under a cold and dry climate on early Mars As you can see here, they start by predicting various aspects of global temperature distribution for different densities of atmosphere. I atmosphere refers to the density of our terrestrial atmosphere as measured on the planetary surface. Note that the current figure would be ~0.01 atmosphere on Mars today.
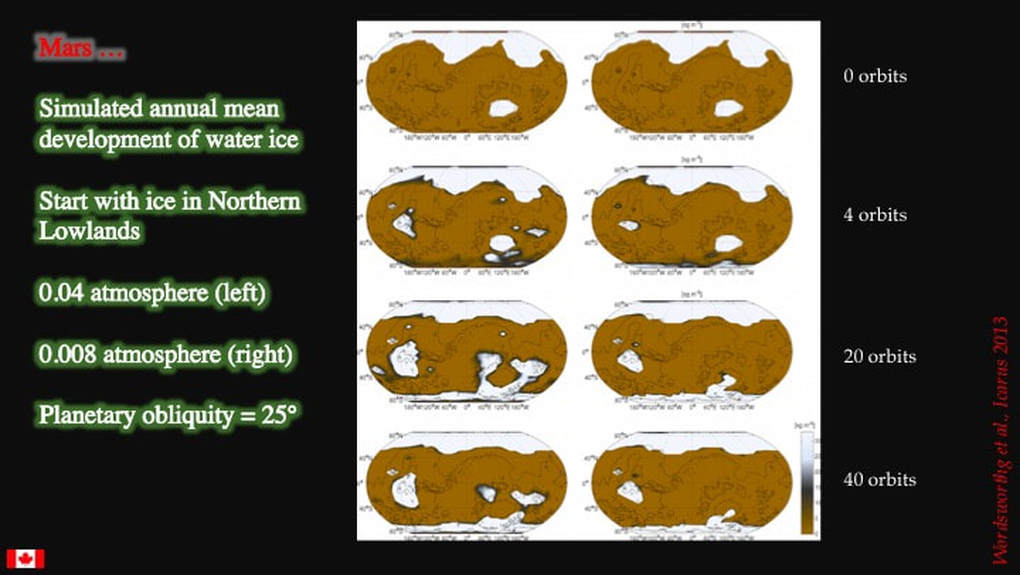
Then they apply these temperatures to simulate the development of water ice over the planetary surface through a time frame of up to 40 average martian years (top to bottom). In this example they model two very thin CO2-rich atmospheres plus water vapour on a planet with the same inclination of the martian rotation axis as we see today. (~23°). Nothing much happens here, except for a very slow transfer by sublimation of some water ice from north to south, with minor ice build-up in the northern parts of the Southern Uplands. Their conclusion ? - low pressure atmospheres don’t produce the required results.
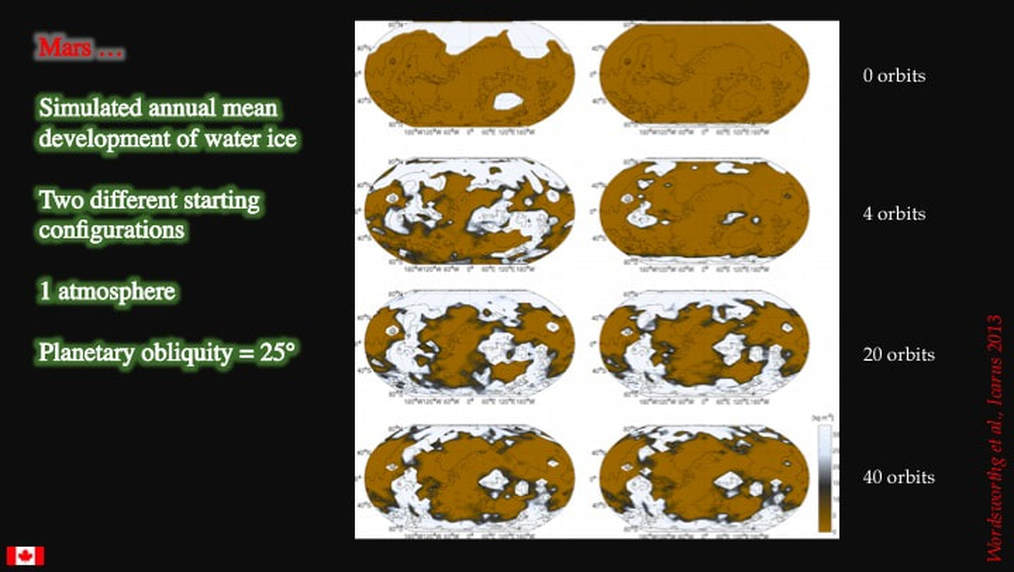
In this example, they changed the starting configuration for the simulation on the right : they put all the starting ice at the poles only. They also increased the CO2-rich atmospheric pressure to one full Earth atmosphere. This is more interesting : note the significant transfer and build-up of water ice in the Southern Uplands. Atmospheric pressure is clearly key to ice transfer, but still maintained a cold and dry climate. Note also that the starting configuration doesn’t have much effect on the overall result.
In this last example, they went to town! They started with ice at the poles, tipped the planet over to an obliquity of 45°, and messed with the topography: they got rid of the Tharsis rise in the left column. Et voilà, they got what they were looking for; major water ice transfer by sublimation to the southern hemisphere and major build –up in the northern parts of the Southern Highlands. The presence or absence of the Tharsis rise did have an effect on ice distribution, but not on the overall result.
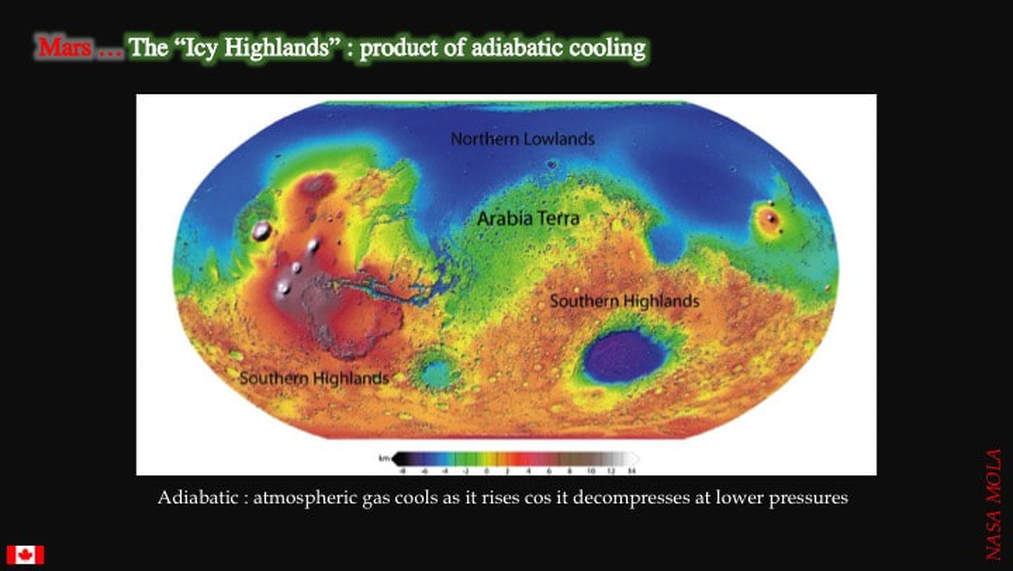
So how did the planetary scientists interpret their results ? Without a large moon, such as Earth’s, Mars precesses chaotically: its spin axis can easily precess to 70° over <100,000 year time frames. At high obliquities, the poles are anomalously warm, while the sub-equatorial highlands are anomalously cold. Hence, water ice sublimates at the poles and migrates equatorially. A good part of this “Icy Highlands” effect is due to “adiabatic cooling”, which is a fancy phrase that says that a gas cools as it expands. This is why you have a compressor in your fridge, and why clouds form over high ground. When atmospheric gases rise on Mars, they decompress and cool, and will precipitate snow over the Southern Highlands - because that’s what atmospheric gases do when they rise over mountains. As an interesting twist to the story, one of the reasons this particular climate model was developed in the first place was because warm and wet climate models predict lots of precipitation over Arabia Terra - and at the time there were few sightings of channels there. The cold and dry model corrected that by predicting minimal ice accumulation in Arabia Terra.
Well, guess what ? In 2016 another group of scientists took another look and found all sorts of evidence for abundant rivers, streams, and even lakes in Arabia Terra - leading some other scientists to claim that this provided support for the wet and warm model and put paid to the cold and dry model for early Mars !
As I said, the debate continues. But let’s just stop and think for a minute here. What about the purported northern ocean ? Its existence is controversial, even highly controversial. However, if it existed, it had to be liquid (deltas, tsunamis) and it would’ve supported a global hydrological cycle. Now ask yourselves: what exactly is this debate about ? From my perspective it pits direct, observational evidence against computer models of climate development. No one is challenging the existence of Noachian river systems, lakes and deltas. The northern ocean and its shoreline are contentious, but constitute a serious hypothesis. In addition it would be difficult for climate modellers to call their computer models into question since they are essentially the same as those that play a central role in climate science here on Earth - with all that that implies, both scientifically and politically.
I always like to leave you with a take-home message – and here it’s this: Martian climate science is challenging the warm and wet model for the climate of early Mars. While it cannot easily simulate the warm and wet climate model, it seems to successfully simulate some aspects of the cold and dry model. However, neither model has the upper hand in this on-going debate. I suggest that the potentially most fruitful avenue of endeavour to help decide between these competing, computer-based climate scenarios would be to reinvest in further direct, observational research to resolve the question: was there, or was there not, a long-term, liquid Noachian ocean on Mars? If it existed, it required a warm and wet global climate.
I always like to leave you with a take-home message – and here it’s this: Martian climate science is challenging the warm and wet model for the climate of early Mars. While it cannot easily simulate the warm and wet climate model, it seems to successfully simulate some aspects of the cold and dry model. However, neither model has the upper hand in this on-going debate. I suggest that the potentially most fruitful avenue of endeavour to help decide between these competing, computer-based climate scenarios would be to reinvest in further direct, observational research to resolve the question: was there, or was there not, a long-term, liquid Noachian ocean on Mars? If it existed, it required a warm and wet global climate.
Proudly powered by Weebly